Chủ đề diện tích hình thang vuông: Diện tích hình thang vuông là 1 định nghĩa toán học tập cực kỳ cần thiết và hữu ích vô cuộc sống thường ngày mỗi ngày. Để tính diện tích hình thang vuông, tất cả chúng ta chỉ việc tiến hành công thức đơn giản: khoảng nằm trong nhì cạnh lòng nhân với độ cao thân thiết nhì lòng. Không chỉ gom tất cả chúng ta đo lường và tính toán đúng chuẩn diện tích S một hình thang, công thức này còn khiến cho tất cả chúng ta nâng cấp kĩ năng trí tuệ logic và tạo nên trong những việc xử lý những câu hỏi toán học tập không giống.
Hình thang vuông với diện tích S được xem bởi vì công thức nào?
Công thức tính diện tích hình thang vuông là: S = 1⁄2 h (a + b), vô cơ S là diện tích S hình thang, h là độ cao, a và b là chừng lâu năm nhì cạnh lòng.
Để tính diện tích hình thang vuông, tớ hoàn toàn có thể vận dụng quá trình sau đây:
1. Xác lăm le độ cao của hình thang vuông: Chiều cao là đoạn trực tiếp vuông góc với nhì lòng và nối bọn chúng.
2. Xác lăm le chừng lâu năm nhì cạnh đáy: Độ lâu năm những cạnh lòng được xác lập bởi vì đoạn trực tiếp nối những điểm kết thúc đẩy của cạnh lòng.
3. kề dụng công thức tính diện tích S: Sử dụng công thức S = 1⁄2 h (a + b) và thay cho vô độ quý hiếm h, a và b đang được xác lập ở quá trình trước, đo lường và tính toán diện tích hình thang vuông.
Ví dụ, fake sử độ cao của hình thang vuông là 5 centimet, chừng lâu năm lòng bên dưới là 8 centimet và chừng lâu năm lòng bên trên là 4 centimet. Theo công thức tính diện tích S, tớ có:
S = 1⁄2 * 5 * (8 + 4) = 1⁄2 * 5 * 12 = 30 cm².
Vậy diện tích hình thang vuông vô ví dụ bên trên là 30 cm².
Bạn đang xem: diện tích hình thang vuông

Công thức tính diện tích hình thang vuông là gì?
Công thức tính diện tích hình thang vuông là: S = 1⁄2 h (a + b). Để tính diện tích hình thang vuông, chúng ta cần phải biết độ cao h của hình thang và 2 lòng a và b của chính nó.
Bước 1: Xác lăm le độ cao h của hình thang. Đây là đoạn trực tiếp nối kể từ đỉnh của hình thang xuống đường thẳng liền mạch tuy vậy song với 2 lòng.
Bước 2: Xác lăm le chừng lâu năm lòng a và b của hình thang. Đây là đoạn trực tiếp ở ngang bên trên và bên dưới của hình thang.
Bước 3: kề dụng công thức S = 1⁄2 h (a + b) nhằm tính diện tích S. Nhân độ cao h với tổng chừng lâu năm 2 lòng a và b, tiếp sau đó phân chia song thành phẩm nhằm chiếm được diện tích hình thang vuông.
Ví dụ: Nếu độ cao h = 4 centimet, lòng a = 5 centimet và lòng b = 8 centimet, tớ hoàn toàn có thể tính diện tích S bởi vì công thức S = 1⁄2 x 4 x (5 + 8) = 34 cm².
Vậy, công thức tính diện tích hình thang vuông là S = 1⁄2 h (a + b).
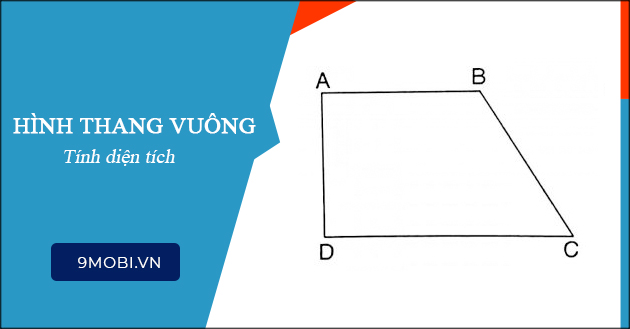
Hình thang vuông với những bộ phận nào?
Hình thang vuông bao gồm những bộ phận sau:
1. Đáy rộng lớn (a): Đây là cạnh có tính lâu năm dài ra hơn nữa vô hình thang vuông.
2. Đáy nhỏ (b): Đây là cạnh có tính lâu năm ngắn lại vô hình thang vuông.
3. Chiều cao (h): Đây là đường thẳng liền mạch vuông góc nối nhì đỉnh của nhì lòng, có tính lâu năm thắt chặt và cố định và trực thuộc hình thang vuông.
4. Hai cạnh mặt mũi (các cạnh đối lập chiều cao): Đây là nhì cạnh nối từng đỉnh của lòng rộng lớn với đỉnh ứng bên trên lòng nhỏ.
5. Đỉnh (A, B): Đây là nhì điểm phía trên lòng rộng lớn và lòng nhỏ, ứng với đầu nhì cạnh mặt mũi.
Công thức tính diện tích hình thang vuông là: S = 1⁄2 h (a + b), vô cơ S là diện tích S, h là độ cao, a và b là chừng lâu năm nhì lòng.

Cách tính diện tích hình thang vuông dựa vào công thức nào?
Để tính diện tích hình thang vuông, tớ dùng công thức sau:
S = một nửa h (a + b)
Trong đó:
- S là diện tích hình thang vuông,
- h là độ cao của hình thang vuông,
- a và b thứu tự là nhì cạnh lòng của hình thang vuông.
Công thức này lấy nửa tích của tổng nhì cạnh lòng và độ cao ứng với nhì cạnh lòng nhằm tính diện tích hình thang vuông.
Diện tích hình thang vuông bởi vì từng nào Phần Trăm diện tích S hình thang thường?
Để tính diện tích hình thang vuông, tớ dùng công thức:
S = một nửa * h * (a + b),
Trong đó:
S là diện tích hình thang vuông,
a và b là chừng lâu năm nhì lòng của hình thang vuông,
h là độ cao của hình thang vuông.
Để tính diện tích S hình thang thông thường, tớ cũng dùng công thức tương tự:
S\' = một nửa * h\' * (a + b),
Trong đó:
S\' là diện tích S hình thang thông thường,
a và b là chừng lâu năm nhì lòng của hình thang thông thường,
h\' là độ cao của hình thang thông thường.
Vậy nhằm đối chiếu diện tích hình thang vuông và diện tích S hình thang thông thường, tớ tiếp tục tính tỉ trọng thân thiết S và S\'. Khi tớ phân chia S mang lại S\', tớ được:
(S / S\') = (1/2 * h * (a + b)) / (1/2 * h\' * (a + b)),
Với (1/2 * (a + b)) kết phù hợp với (1/2 * (a + b)), bọn chúng tiếp tục bị loại bỏ quăng quật và tớ tiếp tục có:
(S / S\') = h / h\'.
Từ trên đây, tớ thấy rằng tỉ trọng diện tích S toàn thân thang vuông và hình thang thông thường là bởi vì tỉ trọng độ cao của nhì hình thang này. Vì vậy, diện tích hình thang vuông bởi vì từng nào Phần Trăm diện tích S hình thang thông thường đó là bởi vì tỉ trọng độ cao thân thiết nhì hình thang.
_HOOK_
Công thức tính diện tích hình thang vuông | toán 2 3 4 5 8
Hãy mày mò công thức tính diện tích hình thang vuông trải qua đoạn phim này. quý khách tiếp tục làm rõ rộng lớn về kiểu cách tính diện tích S và vận dụng kỹ năng phải chăng vô câu hỏi. Hãy nằm trong coi ngay!
[Toán nâng lên 5] Diện tích hình thang - Thầy Khải- SĐT: 0943734664
Muốn nắm rõ Toán nâng lên 5? Video này tiếp tục khiến cho bạn hiểu thâm thúy rộng lớn về những định nghĩa Toán nâng lên cùng theo với những câu hỏi thú vị. Hãy nằm trong theo đuổi dõi nhằm tập luyện khả năng Toán của tôi nhé!
Làm thế này nhằm tính diện tích hình thang vuông Khi chỉ biết độ cao và lòng trên?
Để tính diện tích hình thang vuông Khi chỉ biết độ cao và lòng bên trên, tớ hoàn toàn có thể vận dụng công thức sau:
Diện tích hình thang vuông (S) = một nửa x độ cao (h) x tổng nhì lòng (a + b)
Với a là lòng bên trên và b là lòng bên dưới của hình thang.
- Cách 1: Xác định vị trị của độ cao (h) và lòng bên trên (a).
- Cách 2: Xác định vị trị của lòng bên dưới (b).
- Cách 3: Tính tổng nhì lòng (a + b).
- Cách 4: Tính tích của tổng nhì lòng với độ cao (h).
- Cách 5: Nhân thành phẩm với một nửa nhằm tính diện tích hình thang vuông (S).
Ví dụ: Giả sử tớ với hình thang vuông với độ cao là 5 đơn vị chức năng và lòng bên trên là 8 đơn vị chức năng. Ta cần thiết lần diện tích S của hình thang này.
- Chiều cao (h) = 5 đơn vị
- Đáy bên trên (a) = 8 đơn vị
Giá trị của lòng bên dưới (b) không được hỗ trợ.
- Cách 3: Ta cần thiết lần độ quý hiếm của lòng bên dưới (b). Nếu không tồn tại vấn đề ví dụ, tớ ko thể tính đúng chuẩn diện tích hình thang vuông.
Vì vậy, nhằm tính diện tích hình thang vuông, cần phải có vấn đề về cả độ cao và cả nhì lòng của hình thang.
Công thức tính diện tích hình thang vuông với vận dụng cho tất cả hình thang nghiêng không?
Công thức tính diện tích hình thang vuông với vận dụng cho tất cả hình thang nghiêng ko. Để tính diện tích hình thang vuông, tất cả chúng ta tiếp tục dùng công thức sau:
S = một nửa * h * (a + b)
Trong đó:
- S là diện tích hình thang vuông
- h là độ cao của hình thang vuông
- a và b là chừng lâu năm nhì cạnh lòng của hình thang vuông
Công thức bên trên vận dụng mang lại toàn bộ những hình thang vuông, bao hàm cả hình thang nghiêng. Để tính diện tích S hình thang nghiêng, tớ chỉ cần phải biết độ cao và chừng lâu năm nhì cạnh lòng của hình thang và thay cho vô công thức bên trên, tiếp sau đó tiến hành những luật lệ tính nhằm lần rời khỏi diện tích S.
Ví dụ, nếu như độ cao của hình thang là 5cm, cạnh lòng a là 10cm và cạnh lòng b là 8cm, tớ hoàn toàn có thể tính diện tích S như sau:
S = một nửa * 5 * (10 + 8)
= một nửa * 5 * 18
= 45
Vậy diện tích S hình thang nghiêng vô ví dụ bên trên là 45cm^2.

Tại sao công thức tính diện tích hình thang vuông lại là khoảng nằm trong 2 lòng nhân với chiều cao?
Công thức tính diện tích hình thang vuông là khoảng nằm trong 2 lòng nhân với độ cao vì như thế nó dựa vào nguyên tắc của hình thang thông thường. Trong hình thang thông thường, diện tích S được xem bằng phương pháp lấy khoảng nằm trong của chừng lâu năm nhì lòng và nhân với độ cao ứng với nhì lòng cơ.
Bằng cơ hội tương tự động, vô hình thang vuông, cả nhì lòng đều phải có chừng lâu năm đều bằng nhau và vuông góc với độ cao. Do cơ, tất cả chúng ta hoàn toàn có thể coi hình thang vuông như thể nhì tam giác nằm trong lòng với độ cao thấp kiểu như nhau ghép lại nhau.
Khi tính diện tích S của hình thang vuông, tất cả chúng ta hoàn toàn có thể Reviews nó như thể diện tích S của một tam giác nằm trong lòng và độ cao ứng với cùng 1 lòng, và tiếp sau đó nhân thành phẩm cơ với nhì. Công thức khoảng nằm trong nhì lòng nhân với độ cao đó là phương pháp tính diện tích S của nhì tam giác ghép lại vô hình thang vuông.
Xem thêm: notepad++ download
Ghi ghi nhớ công thức tính diện tích S của 7 hình sau đây khiến cho bạn học tập xuất sắc môn Toán
Cậu mạnh mẽ và tự tin tính diện tích S không? Đến với đoạn phim này, cậu sẽ tiến hành phân tích và lý giải cụ thể về công thức tính diện tích S và vận dụng vô những dạng bài xích tập luyện thực tiễn. Hãy coi đoạn phim ngay lập tức nhằm phát triển thành Chuyên Viên tính diện tích!
Có cơ hội này không giống nhằm tính diện tích hình thang vuông ko dùng công thức trên?
Có, ngoài công thức truyền thống cuội nguồn nhằm tính diện tích hình thang vuông bằng phương pháp lấy khoảng nằm trong của nhì cạnh lòng nhân với độ cao, còn tồn tại một cách tiếp theo nhằm tính diện tích hình thang vuông.
Cách này dùng những lối chéo cánh của hình thang vuông nhằm tính diện tích S. Cụ thể, tớ với công thức tính diện tích hình thang vuông bởi vì nửa tích của tích hai tuyến phố chéo:
S = một nửa × d1 × d2
Trong cơ d1 và d2 thứu tự là chừng lâu năm hai tuyến phố chéo cánh của hình thang vuông. Đường chéo cánh là 1 đoạn trực tiếp nối nhì đỉnh ko kề nhau của hình thang.
Để tính được diện tích hình thang vuông bằng phương pháp này, chúng ta cần phải biết chừng lâu năm hai tuyến phố chéo cánh của hình thang. Sau Khi có mức giá trị của d1 và d2, chúng ta chỉ việc thay cho vô công thức và đo lường và tính toán, tiếp tục chiếm được diện tích S của hình thang vuông.
Đây là 1 phương pháp tính diện tích hình thang vuông không giống nhưng mà ko dùng công thức truyền thống cuội nguồn.
Diện tích hình thang vuông với tác động cho tới những tính chất không giống của hình thang không?
Diện tích hình thang vuông ko tác động thẳng cho tới những tính chất không giống của hình thang như chừng lâu năm những cạnh và góc của hình thang. Diện tích chỉ đơn giản là 1 thông số kỹ thuật biểu thị mang lại diện tích S mặt phẳng của hình thang.
Tuy nhiên, việc tính diện tích hình thang vuông cần dùng những thông số kỹ thuật không giống của hình thang như chừng lâu năm nhì cạnh lòng và độ cao. Vấn đề này Tức là nhằm tính diện tích hình thang vuông, tớ cần phải biết những thông số kỹ thuật không giống của hình thang.
Do cơ, việc tính diện tích hình thang vuông hoàn toàn có thể thêm phần vô việc hiểu và đo lường và tính toán những tính chất không giống của hình thang như chu vi, những góc và những tính chất tương quan không giống. Tuy nhiên, diện tích S ko thực hiện thay cho thay đổi những tính chất này nhưng mà chỉ là 1 thông số kỹ thuật biểu thị mang lại diện tích S mặt phẳng của hình thang.
_HOOK_
Nếu diện tích S hình thang thay cho thay đổi thì độ cao và lòng cũng cần thay cho thay đổi theo đuổi nằm trong tỉ trọng hoặc không?
Nếu diện tích S hình thang thay cho thay đổi, thì độ cao và chừng lâu năm của nhì lòng cũng cần thay cho thay đổi theo đuổi nằm trong tỉ trọng. Vấn đề này được gọi là nguyên tắc đồng tỉ trọng thân thiết diện tích S và những cạnh của hình thang.
Để minh họa điều này, fake sử độ cao của hình thang là h, lòng bên dưới có tính lâu năm là a, và lòng bên trên có tính lâu năm là b. Ta với công thức tính diện tích S của hình thang là S = một nửa * h * (a + b).
Giả sử tớ mong muốn tăng diện tích S của hình thang lên gấp rất nhiều lần. Để thực hiện điều này, tớ hoàn toàn có thể tăng độ cao h lên gấp rất nhiều lần. Lúc này, tớ với diện tích S mới nhất S\' = một nửa * (2h) * (a + b) = 2 * (1/2 * h * (a + b)) = 2S.
Như vậy, Khi tăng độ cao lên gấp rất nhiều lần, diện tích S của hình thang cũng tạo thêm gấp rất nhiều lần. Tương tự động, nếu như hạn chế độ cao chuồn 50%, diện tích S của hình thang cũng giảm sút 50%.
Tương tự động, nếu như tớ tăng hoặc hạn chế chừng lâu năm của những cạnh lòng theo đuổi nằm trong tỉ trọng như nhau, diện tích S của hình thang cũng tiếp tục tăng hoặc thuyên giảm tỉ trọng cơ.
Vì vậy, Khi diện tích S của hình thang thay cho thay đổi, độ cao và lòng cũng cần thay cho thay đổi theo đuổi nằm trong tỉ trọng nhằm giữ lại qui định sản phẩm tỉ trọng thân thiết diện tích S và những cạnh của hình thang.

[TOÁN 5] Công thức tính diện tích S hình thang [2a]
Muốn tập luyện khả năng Toán lớp 5? Video này sẽ hỗ trợ cậu làm rõ những câu hỏi cơ bạn dạng vô Toán 5 và hỗ trợ những cách thức giải hiệu suất cao. Hãy theo đuổi dõi đoạn phim nhằm phát triển thành siêu sao Toán học!
Tại sao công thức tính diện tích hình thang vuông chỉ vận dụng mang lại hình thang vuông?
Công thức tính diện tích hình thang vuông - S = 1⁄2 h (a + b) - chỉ vận dụng mang lại hình thang vuông vì như thế những nhân tố vô công thức này chỉ chính mang lại hình dạng thang vuông nhưng mà ko thích hợp cho những hình dạng thang không giống.
Trong công thức này, \"h\" đại diện thay mặt mang lại độ cao của hình thang. Trong hình thang vuông, hai tuyến phố cao kể từ nhì đỉnh của hình thang đối nhau là và một đường thẳng liền mạch, nên chỉ việc một độ quý hiếm có một không hai nhằm màn trình diễn độ cao. Tuy nhiên, vô hình thang ko vuông, hai tuyến phố cao này sẽ không và một đường thẳng liền mạch, bởi vậy độ cao tiếp tục không giống nhau tùy nằm trong vô địa điểm của điểm hạ cao so với từng lòng của hình thang.
Thêm vô cơ, \"a\" và \"b\" đại diện thay mặt mang lại chừng lâu năm nhì lòng của hình thang. Trong hình thang vuông, nhì lòng là lòng rộng lớn và lòng nhỏ đều vuông góc với độ cao và tuy vậy song cùng nhau. Tuy nhiên, vô hình thang ko vuông, những lòng sẽ không còn nhất thiết cần vuông góc với độ cao và cũng ko cần tuy vậy song cùng nhau. Do cơ, công thức tính diện tích hình thang vuông ko được vận dụng cho những hình dạng thang không giống.
Có công thức này nhằm tính tổng diện tích S của không ít hình thang vuông không?
Có, nhằm tính tổng diện tích S của không ít hình thang vuông, bạn cũng có thể dùng công thức sau:
Tổng diện tích S = Diện tích hình thang vuông 1 + Diện tích hình thang vuông 2 + ... + Diện tích hình thang vuông n
Với từng hình thang vuông, bạn cũng có thể dùng công thức nhằm tính diện tích:
Diện tích hình thang vuông = một nửa x (cạnh lòng 1 + cạnh lòng 2) x chiều cao
Bạn hoàn toàn có thể vận dụng công thức này mang lại từng hình thang vuông vô tổng số hình thang vuông nhưng mà bạn thích tính tổng diện tích S. Sau cơ, nằm trong toàn bộ những diện tích S lại cùng nhau sẽ được tổng diện tích S của không ít hình thang vuông.
Ví dụ:
Giả sử chúng ta với nhì hình thang vuông với những độ quý hiếm như sau:
Hình thang vuông 1: Cạnh lòng 1 = 3, cạnh lòng 2 = 7, độ cao = 4
Hình thang vuông 2: Cạnh lòng 1 = 5, cạnh lòng 2 = 9, độ cao = 6
Để tính tổng diện tích S của nhì hình thang vuông này, chúng ta vận dụng công thức như sau:
Diện tích hình thang vuông 1 = một nửa x (3 + 7) x 4 = 20
Diện tích hình thang vuông 2 = một nửa x (5 + 9) x 6 = 42
Tổng diện tích S = đôi mươi + 42 = 62
Vậy tổng diện tích S của nhì hình thang vuông bên trên là 62 đơn vị chức năng diện tích S.

Diện tích hình thang vuông với phần mềm vô cuộc sống mỗi ngày như vậy nào?
Diện tích hình thang vuông được xem bởi vì công thức S = một nửa h (a + b), vô cơ h là độ cao, a và b là chừng lâu năm nhì cạnh lòng của hình thang vuông. Diện tích hình thang vuông với phần mềm vô cuộc sống mỗi ngày như sau:
1. Xây dựng và loài kiến trúc: Diện tích hình thang vuông cực kỳ hữu ích trong những việc đo lường và tính toán lượng và vật tư quan trọng cho những công trình xây dựng thi công, như lát gạch men, thực thi sàn, chân móng và những công trình xây dựng bản vẽ xây dựng không giống.
2. Thiết tiếp nội thất: Diện tích hình thang vuông hoàn toàn có thể được dùng nhằm đo lường và tính toán độ cao thấp và diện tích S của những vật tư thiết kế bên trong như tấm ván, vải vóc hoặc domain authority nhằm design và phát triển ghế, bàn, tủ và những vật thiết kế bên trong không giống.
3. Chuẩn bị menu và nấu nướng ăn: Trong việc nấu bếp, diện tích hình thang vuông hoàn toàn có thể được dùng nhằm đo lường và tính toán lượng vật liệu quan trọng cho những công thức nấu bếp và pha trộn, như diện tích S vụn bột, diện tích S bánh mỳ hoặc những vật liệu không giống.
4. Lập plan mang lại không khí và vùng trồng trọt: Diện tích hình thang vuông hoàn toàn có thể được vận dụng vô lập plan và design không khí vườn hoặc nông trại nhằm đo lường và tính toán diện tích S của những điểm trồng trọt, vườn cây hoặc sảnh nghịch ngợm, kể từ cơ gom quy hướng và bố trí một cơ hội hiệu suất cao.
5. Tính toán diện tích S vô hình thể thao: Diện tích hình thang vuông cũng hoàn toàn có thể được dùng nhằm đo lường và tính toán diện tích S sảnh và những điểm không giống trong số môn thể thao như đá bóng, bóng chuyền, sảnh golf và sảnh tennis.
Tóm lại, diện tích hình thang vuông có tương đối nhiều phần mềm vô cuộc sống mỗi ngày, kể từ thi công bản vẽ xây dựng cho tới nấu bếp, design không khí và những hoạt động và sinh hoạt thể thao. Việc hiểu và biết phương pháp đo lường và tính toán diện tích hình thang vuông sẽ hỗ trợ tất cả chúng ta vận dụng nó một cơ hội hiệu suất cao và tiện lợi trong số hoạt động và sinh hoạt mỗi ngày.
Có thể lần diện tích hình thang vuông bằng phương pháp trực quan lại hoá hình thang và đo bởi vì khí cụ giám sát và đo lường không?
Có thể lần diện tích hình thang vuông bằng phương pháp trực quan lại hoá hình thang và đo bởi vì khí cụ giám sát và đo lường. Tuy nhiên, cơ hội này sẽ không đáp ứng tính đúng chuẩn và hoàn toàn có thể kéo theo sơ sót vô thành phẩm.
Để tính diện tích hình thang vuông một cơ hội đúng chuẩn, tớ hoàn toàn có thể dùng công thức tính diện tích S. Công thức mang lại diện tích hình thang vuông là:
S = 1⁄2 h (a + b).
Trong đó:
- S là diện tích hình thang vuông.
- h là độ cao của hình thang.
- a, b là chừng lâu năm nhì lòng của hình thang.
Để tính diện tích S, tớ chỉ cần phải biết độ cao và chừng lâu năm nhì lòng của hình thang và tiến hành luật lệ tính theo đuổi công thức bên trên. Sau cơ, tớ sẽ có được thành phẩm là diện tích hình thang vuông.
Ví dụ:
Giả sử với cùng 1 hình thang vuông với độ cao là 5 centimet, chừng lâu năm lòng bên trên là 8 centimet và chừng lâu năm lòng bên dưới là 12 centimet. Ta hoàn toàn có thể tính diện tích S của hình thang vuông như sau:
S = 1⁄2 * 5 * (8 + 12) = 1⁄2 * 5 * đôi mươi = 50 cm².
Do cơ, diện tích S của hình thang vuông vô ví dụ này là 50 cm².

Xem thêm: cách nạp robux
_HOOK_
Diện tích hình thang - Bài 4 - Toán học tập 8 - Cô Phạm Thị Huệ Chi (HAY NHẤT)
Bạn đang được học tập Toán học tập lớp 8 và gặp gỡ trở ngại ở Bài 4? Video này tiếp tục khiến cho bạn làm rõ câu hỏi và hỗ trợ những cách thức giải câu hỏi hiệu suất cao. Hãy nằm trong coi đoạn phim nhằm băng qua trở ngại và thành công xuất sắc vô Toán học!
Đang xử lý...











Bình luận