Số lượt phát âm bài xích viết: 166.426
7 hằng đẳng thức lưu niệm là những đẳng thức cơ phiên bản được minh chứng vị phép tắc nhân nhiều thức với khá nhiều thức, được dùng thông thường xuyên nhằm giải phương trình, nhân phân tách những nhiều thức… Trong nội dung bài viết tiếp sau đây, DINHNGHIA.VN tiếp tục giúp cho bạn tổ hợp 7 hằng đẳng thức lưu niệm đúng đắn, khá đầy đủ kể từ cơ phiên bản cho tới không ngừng mở rộng nâng lên, nằm trong thám thính hiểu nhé!.
Bạn đang xem: hằng đẳng thức mở rộng
Tìm hiểu 7 hằng đẳng thức lưu niệm cơ bản
Trong toán học tập, hằng đẳng thức xứng đáng nhớ là những đẳng thức cơ phiên bản được minh chứng vị phép tắc nhân nhiều thức với khá nhiều thức. Những đẳng thức này được dùng thông thường xuyên trong những vấn đề tương quan cho tới giải phương trình, nhân phân tách những nhiều thức, thay đổi biểu thức bên trên cấp cho học tập trung học tập hạ tầng và trung học tập phổ thông.
Tóm tắt 7 hằng đẳng thức xứng đáng nhớ
Trong những hằng đẳng thức này, tao mang trong mình 1 mặt mày vết vị được xem là tổng hoặc hiệu và mặt mày gọi lại là tích hoặc lũy quá. Dưới đó là bảng hằng đẳng thức xứng đáng nhớ dành cho tới bạn:
| Bình phương của một tổng | \((a+b)^{2}= a^{2}+2ab+b^{2}\) |
| Bình phương của một hiệu | \((a-b)^{2}= a^{2}-2ab+b^{2}\) |
| Hiệu nhị bình phương | \(a^{2}-b^{2}=(a+b)(a-b)\) |
| Lập phương của một tổng | \((a+b)^{3}= a^{3}+3a^{2}b +3ab^{2}+b^{3}\) |
| Lập phương của một hiệu | \((a-b)^{3}= a^{3}-3a^{2}b +3ab^{2}-b^{3}\) |
| Tổng nhị lập phương | \(a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\) |
| Hiệu nhị lập phương | \(a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\) |
Phát biểu 7 hằng đẳng thức lưu niệm vị lời
1. Bình phương của một tổng tiếp tục vị bình phương của số loại 1 cùng theo với nhị chuyến tích của số loại nhất với số loại nhị nằm trong bình phương số loại hai
2. Bình phương của một hiệu tiếp tục vị bình phương của số loại 1 trừ gấp đôi tích số loại nhất với số thứ hai cùng theo với bình phương số thứ hai.
3. Hiệu của 2 bình phương tiếp tục vị tích của tổng 2 số với hiệu 2 số.
4. Lập phương của một tổng tiếp tục vị với lập phương số loại 1 + 3 chuyến tích bình phương số loại 1 với số thứ hai + 3 chuyến tích số loại 1 với bình phương số thứ hai + lập phương số thứ hai.
5. Lập phương của một tổng tiếp tục vị với lập phương số loại 1 -3 chuyến tích bình phương số loại 1 với số thứ hai + 3 chuyến tích số loại 1 với bình phương số thứ hai – lập phương số thứ hai.
6. Tổng nhị lập phương tiếp tục vị tích thân thích tổng 2 số với bình phương thiếu hụt của một hiệu.
7. Hiệu của 2 lập phương tiếp tục vị với tích thân thích hiệu nhị số với bình phương thiếu hụt của một tổng.
Các hằng đẳng thức mở rộng thông thường gặp
Hằng đẳng thức lưu niệm với hàm bậc 2
- \((a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc\)
- \((a+b-c)^{2}=a^{2}+b^{2}+c^{2}+2ab-2ac-2bc\)
- \((a-b-c)^{2}=a^{2}+b^{2}+c^{2}-2ab-2ac+2bc\)
Hằng đẳng thức lưu niệm với hàm bậc 3
- \(a^3 + b^3 = (a+b)^3 – 3ab(a + b)\)
- \(a^3 – b^3 = (a – b)^3 + 3ab(a – b)\)
- \((a+b+c)^{3}=a^{3}+b^{3}+c^{3}+3(a+b)(a+c)(b+c)\)
- \(a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)\)
- \((a – b)^3 + (b – c)^3 + (c – a)^3 = 3(a – b)(b – c)(c – a)\)
- \((a + b)(b + c)(c + a) – 8abc = a(b – c)^2 + b(c – a)^2 + c(a – b)^2\)
- \((a + b)(b+c)(c+a) = (a+b+c)(ab+bc+ca)-abc\)
- \((a + b)(b + c)(c + a) – 8abc = a(b – c)^2 + b(c – a)^2 + c(a – b)^2\)
- \((a + b)(b+c)(c+a) = (a+b+c)(ab+bc+ca)-abc\)
Hằng đẳng thức dạng tổng quát
\(a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^{2}-a^{n-4}b^{3}+…+a^{2}b^{n-3}-a.b^{n-2}+b^{n-1})\) (1) với n là số lẻ nằm trong tập dượt N
\(a^n – b^n = (a – b)(a^{n – 1} + a^{n – 2}b + a^{n – 3}b^2 + … + a^2b^{n – 3} + ab^{n – 2} + b^{n – 1} )\)
Tìm hiểu nhị thức Newton là gì?
\((a + b)^{n} = \sum_{k = 0}^{n}C^{k}_{n}a^{n – k}b^{k}\)
Với \(a, b \epsilon \mathbb{R}, n \epsilon \mathbb{N}^{*}\)
Xem thêm: Những câu hỏi phổ biến về trang web live bóng đá Vebo TV
Bài tập dượt về 7 hằng đẳng thức xứng đáng nhớ





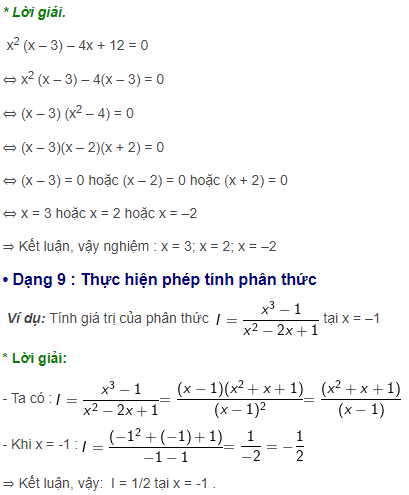
Vận dụng hằng đẳng thức xứng đáng nhớ



Trên đó là nội dung bài viết tổ hợp kỹ năng và kiến thức về những hằng đẳng thức lưu niệm cơ phiên bản và không ngừng mở rộng. Nếu đem góp phần hoặc vướng mắc gì về chủ thể 7 hằng đẳng thức lưu niệm, chúng ta nhớ rằng phản hồi bên dưới nhé! Chúc các bạn luôn luôn học tập tốt!.
Xem thêm thắt >>> Chuyên đề phân tách nhiều thức cho tới nhiều thức: Lý thuyết và Bài tập
Xem thêm thắt >>> Quy tắc nhân đơn thức với khá nhiều thức và Một số dạng bài xích tập
Xem thêm: finger
Xem cụ thể qua quýt bài xích giảng:
(Nguồn: www.youtube.com)
Please follow and lượt thích us:











Bình luận