Giá trị tuyệt đối

Bách khoa toàn thư phanh Wikipedia

Giá trị vô cùng (tiếng Anh: Absolute value) - còn thông thường được gọi là mô-đun (modulus) của một vài thực x được viết lách là |x|, là độ quý hiếm của chính nó tuy nhiên quăng quật vệt. Như vậy |x| = -x nếu như x là số âm (-x là số dương), và |x| = x nếu như x là số dương, và |0| =0. Giá trị vô cùng của một vài hoàn toàn có thể hiểu là khoảng cách của số cơ cho tới số 0.

Bạn đang xem: giá trị tuyệt đối là gì

Trong toán học tập, việc dùng độ quý hiếm tuyệt khái niệm vô một loạt hàm toán học tập, và còn được không ngừng mở rộng cho những số phức, véctơ, ngôi trường,... contact trực tiếp với định nghĩa độ quý hiếm.

Đồ thị của một hàm số với những thay đổi số ở trong vệt "giá trị tuyệt đối" thì luôn luôn trực tiếp ở phía bên trên của trục hoành.

Số thực[sửa | sửa mã nguồn]

Với từng số thực , độ quý hiếm vô cùng của - ký hiệu là - được ấn định nghĩa:

Định nghĩa bên trên đã cho thấy, độ quý hiếm vô cùng của vẫn là một số ko âm.

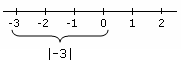
Giá trị tuyết đối của -3 là khoảng cách kể từ điểm -3 tới điểm 0 bên trên đường thẳng liền mạch thực.

Hiểu theo đòi khía cạnh hình học tập, độ quý hiếm vô cùng của một vài thực là khoảng cách kể từ số cơ tới điểm 0 bên trên đường thẳng liền mạch thực (real number line, hay còn gọi là trục số thực). Tổng quát mắng rộng lớn, độ quý hiếm vô cùng thân thích nhị số thực không giống nhau là khoảng cách thân thích bọn chúng bên trên đường thẳng liền mạch thực, ví dụ: |5 - 3| = 2 (khoảng cơ hội thân thích 5 và 3).

Mệnh đề 1 bên dưới đấy là một như nhau thức (identity). Nó tương tự với khái niệm bên trên và đôi lúc hoàn toàn có thể được dùng nhằm khái niệm về độ quý hiếm vô cùng.

MỆNH ĐỀ 1:

MỆNH ĐỀ 2:

Xem thêm: rap chieuphimquocgia

Chứng minh:

Vì và đều to hơn 0 nên hoặc đều nhỏ rộng lớn tổng . Vậy tao luôn luôn có: .

MỆNH ĐỀ 3:

Ta cũng có thể có nhị bất đẳng thức (inequalities) quan tiền trọng:

Hai bất đẳng thức bên trên thông thường được dùng nhằm giải những vấn đề bất đẳng thức không giống. Ví dụ:

Số phức[sửa | sửa mã nguồn]

Vì số phức (complex number) không tồn tại trật tự, nên khái niệm về độ quý hiếm vô cùng của những số phức ko thể được suy đi ra kể từ khái niệm ứng của những số thực. Tuy nhiên, kể từ như nhau thức ở mệnh đề 1 (xem phần số thực ở trên), tao với khái niệm sau:

Xem thêm: luyen violympic