hàm số đồng biến trên khoảng

Hàm số là gì?

Giả sử X và Y' là nhì tụ họp tùy ý. Nếu với 1 quy tắc ƒ mang đến ứng từng x ∈ X với 1 và có một nó ∈ Y thì tớ bảo rằng ƒ là một trong những hàm kể từ X nhập Y, kí hiệu:

Bạn đang xem: hàm số đồng biến trên khoảng

ƒ : X → Y 

X → ƒ(x)

Nếu X, Y là những tụ họp số thì ƒ được gọi là một trong những hàm số. Trong công tác Toán 9 tất cả chúng ta chỉ xét những hàm số thực của những trở thành số thực, tức thị X ⊂ R và Y ⊂ R. X được gọi là tập dượt xác lập (hay miền xác định) của hàm số ƒ. Tập xác lập thông thường được kí hiệu là D.

Số thực x ∈ X được gọi là trở thành số song lập (gọi tắt là trở thành số hoặc đối số). Số thực y = ƒ(x) ∈ Y được gọi là độ quý hiếm của hàm số f bên trên điểm x. Tập thích hợp toàn bộ những độ quý hiếm của ƒ(x) Lúc x lấy từng số thực nằm trong tụ họp X gọi là tập dượt độ quý hiếm (hay miền giá bán trị) của hàm số ƒ.

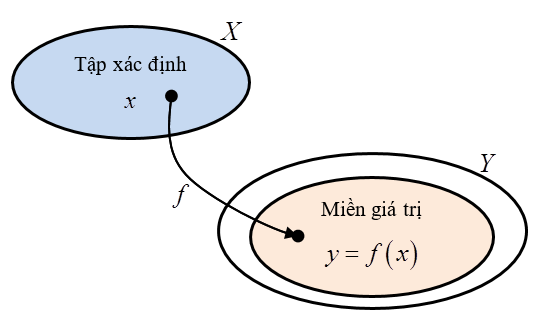
Ta cũng rất có thể khái niệm hàm số như sau: Nếu đại lượng nó tùy thuộc vào đại lượng thay cho thay đổi x sao cho: Với từng độ quý hiếm của x tớ luôn luôn xác lập được có một độ quý hiếm ứng của nó thì nó được gọi là hàm số của x và x được gọi là trở thành số.

Khi x thay cho thay đổi nhưng mà nó luôn luôn nhận một độ quý hiếm thì nó được gọi là hàm hằng. Chẳng hạn, nó = 3 là một trong những hàm hằng.

Kí hiệu: Khi nó là hàm số của x, tớ rất có thể kí hiệu là nó = ƒ(x), hoặc nó = g(x) hoặc nó = h(x),...

Tập xác lập của hàm số nó = ƒ(x) là tập dượt con cái của R bao hàm những độ quý hiếm sao mang đến biểu thức ƒ(x) xác lập.

Định lí về tính chất đồng trở thành nghịch ngợm trở thành của hàm số

Cho hàm số nó = f(x) với đạo hàm bên trên khoảng chừng (a;b). Khi tê liệt hàm số tiếp tục đồng trở thành và nghịch ngợm trở thành với:

- Hàm số nó = f(x) đồng trở thành bên trên khoảng chừng (a;b) Lúc và chỉ Lúc f’(x) ≥ 0 với từng độ quý hiếm x nằm trong khoảng chừng (a;b). Dấu bởi vì xẩy ra bên trên hữu hạn điểm.

- Hàm số nó = f(x) nghịch ngợm trở thành bên trên khoảng chừng (a;b) khi và chỉ Lúc f’(x) ≤ 0 với từng độ quý hiếm x nằm trong khoảng chừng (a;b). Dấu bởi vì xẩy ra bên trên hữu hạn điểm.

Khi này hàm số đồng trở thành bên trên r? hàm số nghịch ngợm trở thành bên trên r Lúc nào?

Trước tiên tất cả chúng ta cần phải biết rằng ĐK nhằm hàm số đồng biến bên trên r, ĐK trước tiên là hàm số cần xác lập bên trên R đang được.

Giả sử hàm số y=f(x) xác lập và liên tiếp và với đạo hàm bên trên R. Khi tê liệt hàm số y=f(x) đơn điệu bên trên R Lúc và chỉ Lúc thỏa mãn nhu cầu nhì ĐK sau:

• Hàm số y=f(x) xác lập bên trên R.

• Hàm số y=f(x) với đạo hàm ko thay đổi vệt bên trên R.

Ở ĐK thứ hai nhằm hàm số đồng trở thành bên trên r tất cả chúng ta cần thiết xem xét là y’ rất có thể bởi vì 0 tuy nhiên chỉ được bởi vì 0 bên trên hữu hạn điểm (hoặc số điểm nhưng mà đạo hàm bởi vì 0 là tập dượt kiểm điểm được).

Một số tình huống ví dụ tất cả chúng ta rất cần phải ghi nhớ về ĐK hàm số luôn luôn đồng trở thành bên trên r, như sau:

Hàm số nhiều thức bậc 1

Hàm số nhiều thức bậc 3

Lưu ý: Hàm số nhiều thức bậc chẵn ko thể đơn điệu bên trên R được, ví dụ như: Hàm số bậc 2, 4,...

Các dạng bài xích tập dượt phần mềm hàm số đồng trở thành nghịch ngợm trở thành bên trên r thông thường gặp

Dưới đó là tổ hợp một số trong những dạng bài xích tập dượt tương quan cho tới ĐK hàm số đồng trở thành bên trên r nhằm những em vận dụng và thực hành:

Dạng 1: Tìm khoảng chừng đồng trở thành – nghịch ngợm trở thành của hàm số

Cho hàm số nó = f(x)

• f’(x) > 0 ở đâu thì hàm số đồng trở thành ở đấy.

• f’(x) < 0 ở đâu thì hàm số nghịch ngợm trở thành ở đấy.

Quy tắc:

• Tính f’(x), giải phương trình f’(x) = 0 thám thính nghiệm.

• Lập bảng xét vệt f’(x)

• Dựa nhập bảng xét vệt và tóm lại.

Ví dụ: Cho hàm số f(x) = -2x3 + 3x2 – 3x và 0 ≤ a < b. Khẳng quyết định này tại đây sai?

A. Hàm số nghịch ngợm trở thành bên trên ℝ

B. f (a) > f (b)

C. f (b) < 0

D. f (a) < f (b)

Hướng dẫn giải: Chọn đáp án D.

Ta có: f’(x) = -6x2 + 6x – 3 < 0, ∀ x ∊ ℝ

⇒ Hàm số nghịch ngợm trở thành bên trên ℝ.

Xem thêm: chang trai cua em tap 15

0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)

Dạng 2: Tìm ĐK của thông số m

Kiến thức chung

• Để hàm số đồng biến trên khoảng (a;b) thì f’(x) ≥ 0, ∀ x ∊ (a;b).

• Để hàm số nghịch ngợm trở thành bên trên khoảng chừng (a;b) thì f’(x) ≤ 0, ∀ x ∊ (a;b).

Chú ý: Cho hàm số y = ax^3 + bx^2 + cx + d

• Khi a > 0 nhằm hàm số nghịch ngợm trở thành bên trên một quãng có tính nhiều năm bởi vì k ⇔ y’ = 0 với 2 nghiệm phân biệt x1, x2 sao mang đến |x1 – x2| = k

• Khi a < 0 nhằm hàm số đồng trở thành bên trên một quãng có tính nhiều năm bởi vì k ⇔ y’ = 0 với 2 nghiệm phân biệt x1, x2  sao mang đến |x1 – x2| = k

Ví dụ: Hàm số nó = x3 – 3x2 + (m – 2) x + 1  luôn luôn đồng trở thành khi:

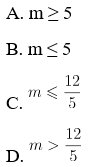
Hướng dẫn giải: Chọn đáp án A.

Ta có: y’ = 3x2 – 6x + m – 2

Hàm số đồng trở thành bên trên ℝ Lúc và chỉ Lúc y’ = 3x2 – 6x + m – 2 ≥ 0, ∀ x ∊ ℝ

⇔ ∆’ ≤ 0 ⇔ 15 – 3m ≤ 0 ⇔ m ≥ 5

Dạng 3: Xét tính đơn điêu hàm số trùng phương

• Bước 1: Tìm tập dượt xác định

• Bước 2: Tính đạo hàm f’(x) = 0. Tìm những điểm xi (i= 1, 2,… n) nhưng mà bên trên tê liệt đạo hàm bởi vì 0 hoặc ko xác lập.

• Bước 3: Sắp xếp những điểm xi theo đòi trật tự tăng dần dần và lập bảng trở thành thiên.

• Bước 4: Nêu tóm lại về những khoảng chừng đồng trở thành, nghịch ngợm trở thành của hàm số.

Ví dụ: Xét tính đơn điệu của từng hàm số sau: nó = -x4 + x2 – 2

Hàm số xác lập với từng x ∊ ℝ

y’ = -4x3 + 2x = 2x (-2x2 + 1)

Cho y’ = 0 ⇒ x = 0 hoặc x = -√2/2 hoặc x = √2/2

Bảng trở thành thiên:

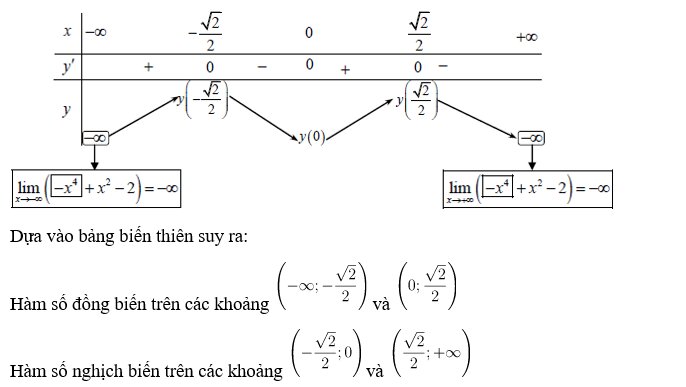
Các bài xích tập dượt khuôn khác

Ví dụ 1: Cho hàm số y=x³+2(m-1)x²+3x-2. Tìm m nhằm hàm đang được mang đến đồng trở thành bên trên R.

Hướng dẫn giải: 

Để y=x³+2(m-1)x²+3x-2  đồng trở thành bên trên R thì (m-1)²-3.3≤0⇔-3≤m-1≤3⇔-2≤m≤4.

Các bạn phải chú ý với hàm nhiều thức bậc 3 với chứa chấp thông số ở thông số bậc tối đa thì tất cả chúng ta cần thiết xét tình huống hàm số suy trở thành.

Ví dụ 2: Cho hàm số y=mx³-mx²-(m+4)x+2. Xác quyết định m nhằm hàm số đang được mang đến nghịch ngợm trở thành bên trên R.

Hướng dẫn giải: 

Ta xét tình huống hàm số suy trở thành. Khi m=0, hàm số trở nên y=-x+2. Đây là hàm hàng đầu nghịch ngợm trở thành bên trên R. Vậy m=0 thỏa mãn nhu cầu đòi hỏi câu hỏi.

Với m≠0, hàm số là hàm nhiều thức bậc 3. Do tê liệt hàm số nghịch ngợm trở thành bên trên R Lúc và chỉ Lúc m<0 đôi khi m²+3m(m+4)≤0. Giải những ĐK rời khỏi tớ được -3≤m<0.

Kết thích hợp 2 tình huống tớ được -3≤m≤0 thỏa mãn nhu cầu đòi hỏi câu hỏi.

Một số bài xích thói quen hàm số đồng trở thành bên trên r và nghịch ngợm trở thành bên trên r tự động luyện

Xem thêm: chân trời sự kiện

Trên đó là toàn bộ những kiến thức và kỹ năng và dạng bài xích tập dượt về hàm số đồng trở thành bên trên r. Ngoài ra Monkey còn bổ sung cập nhật tăng những khái niệm về hàm số rằng công cộng và những dạng hàm số rằng riêng biệt như: Hàm số hàng đầu, hàm số bậc nhì,... Hàm con số giác, hàm số logarit và hàm số nón. Hy vọng với những share bên trên phía trên của Monkey tiếp tục giúp đỡ bạn phần này trong các công việc ôn tập dượt và ghi ghi nhớ những kiến thức và kỹ năng quan trọng trong những kì thi đua, nhất là kì thi đua trung học phổ thông Quốc Gia. Xin được sát cánh đồng hành nằm trong chúng ta.