hệ số góc

By Admin 02/10/2023 0

Gọi A là giao phó điểm của lối thẳng

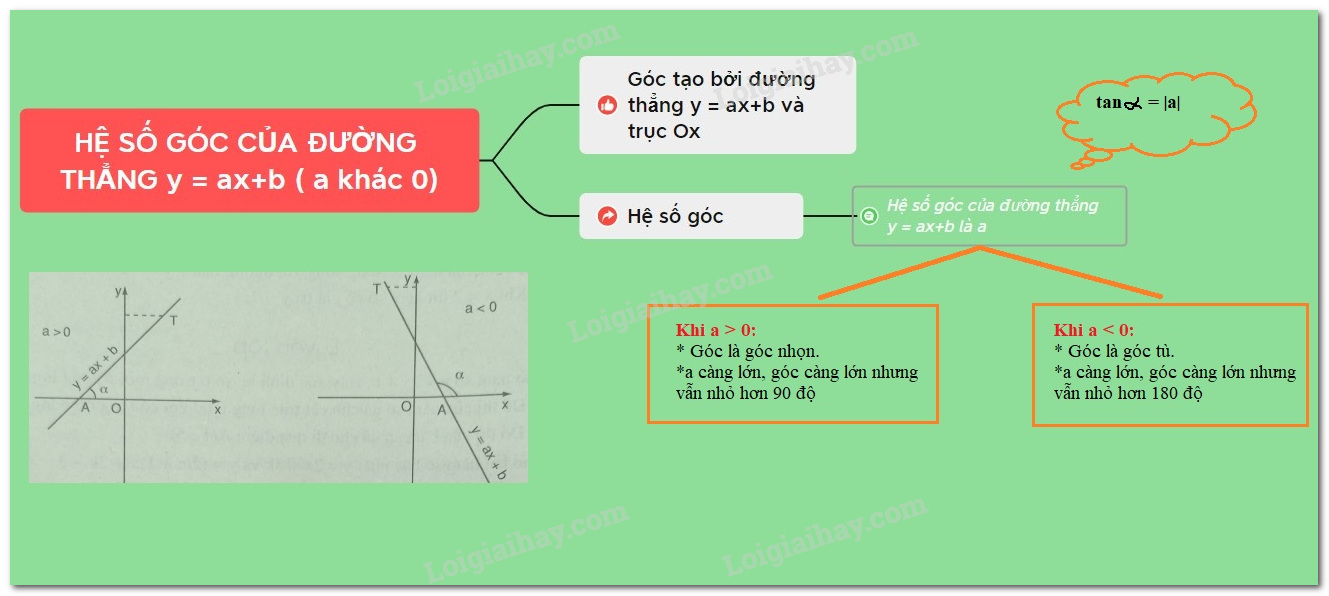
1. Góc tạo nên vị đường thẳng liền mạch \(y = ax + b (a ≠ 0)\) và trục \(Ox.\)

Gọi \(A\) là giao phó điểm của đường thẳng liền mạch \(d:y = ax + b\) với trục \(Ox\) và \(T\) là 1 điểm nằm trong đường thẳng liền mạch, ở phía bên trên trục \(Ox.\) Khi bại liệt góc \(\alpha=\widehat {TAx}\) được gọi là góc tạo nên vị đường thẳng liền mạch \(d: nó = ax + b\) và trục \(Ox.\) 

Bạn đang xem: hệ số góc

 

2. Hệ số góc của đường thẳng liền mạch \(y = ax + b (a ≠ 0)\) 

+) Khi \(a > 0,\) góc tạo nên vị đường thẳng liền mạch \(y = ax + b\) và trục \(Ox\) là góc nhọn và nếu như \(a\) càng rộng lớn thì góc bại liệt càng rộng lớn vẫn nhỏ rộng lớn \(90^0.\)

+) Khi \(a < 0,\) góc tạo nên vị đường thẳng liền mạch \(y = ax + b\) và trục \(Ox\) là góc tù và nếu như \(|a|\) càng nhỏ nhắn thì góc bại liệt càng rộng lớn vẫn nhỏ rộng lớn \(180^0.\)

Như vậy, góc tạo nên vị đường thẳng liền mạch \(d: nó = ax + b\) và trục \(Ox\) tùy thuộc vào \(a.\)

Người tớ gọi \(a\) là hệ số góc của đường thẳng liền mạch \(y = ax + b.\)

Lưu ý:

+) Khi \(a > 0,\) tớ sở hữu \(\tan \alpha= a.\)

+) Khi \(a < 0,\) tớ sở hữu \(\tan (180^0-\alpha) = -a.\)

Từ bại liệt tìm kiếm được số đo của góc \(180^0-\alpha\) rồi suy rời khỏi số đo của góc \(\alpha.\)

+) Các đường thẳng liền mạch sở hữu nằm trong thông số \(a\) (\(a\) là thông số của \(x\)) thì tạo nên với trục \(Ox\) những góc cân nhau.

3. Các dạng toán cơ bản

Dạng 1: Xác ấn định hệ số góc của lối thẳng

Phương pháp:

Đường trực tiếp \((d)\) sở hữu phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) sở hữu \(a\) là hệ số góc.

Ví dụ: Hệ số góc của đường thẳng liền mạch \(y=-2x+1\) là \(a=-2\)

Dạng 2: Tính góc tạo nên vị tia \(Ox\) và đường thẳng liền mạch \((d).\)

Phương pháp:

Gọi \(\alpha \) là góc tạo nên vị tia \(Ox\) và \(d.\) Ta có: \(a = \tan \alpha \)

Xem thêm: bài hát đồ dùng bé yêu

Ví dụ: Góc tạo nên vị tia \(Ox\) và đường thẳng liền mạch \((d):y=\sqrt 3 x+1\) là \(\alpha \)

Khi đó: \(\tan \alpha=\sqrt 3\) nên \(\alpha =60^0\)

Dạng 3. Viết phương trình đường thẳng liền mạch hoặc dò thám thông số m lúc biết hệ số góc

Phương pháp:

Gọi phương trình  đường trực tiếp cần thiết dò thám là $y = ax + b\,\,\left( {a \ne 0} \right)$.

Dựa nhập lý thuyết về hệ số góc nhằm tìm $a$. Từ bại liệt, dùng dữ khiếu nại sót lại của đề bài bác nhằm tìm $b$.


Bình luận

Chia sẻ

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Xem thêm: chang trai cua em tap 15

Báo lỗi - Góp ý

Tham Gia Group Zalo 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện nhập lớp 10 bên trên Tuyensinh247.com, khẳng định hùn học viên lớp 9 học tập chất lượng, trả trả khoản học phí nếu như học tập ko hiệu suất cao.