chu vi hình tam giác

Chu vi hình tam giác là kiến thức và kỹ năng Toán học tập căn phiên bản và được tiến hành lịch trình Toán học tập lớp 2. Chu vi hình tam giác được xem theo đuổi từng loại hình tam giác không giống nhau, bao gồm hình tam giác thông thường, tam giác vuông, tam giác đều và tam giác cân nặng. Công thức tính chu vi hình tam giác tiếp tục giản dị rộng lớn công thức tính diện tích S hình tam giác. Dưới đấy là công thức tính chu vi hình tam giác với rất nhiều hình không giống nhau.

1. Tính chu vi tam giác thường

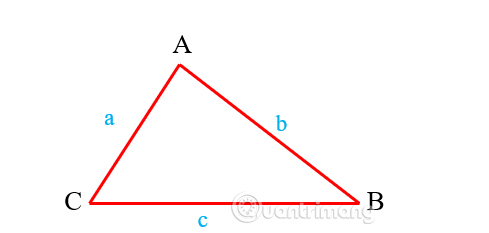
Tam giác thông thường là tam giác cơ phiên bản sở hữu 3 cạnh với phỏng nhiều năm không giống nhau. Công thức tính chu vi hình tam giác thường:

Bạn đang xem: chu vi hình tam giác

P = a + b + c

Trong đó:

• P là chu vi tam giác.
• a, b, c là 3 cạnh của hình tam giác tê liệt.

Để tính diện tích S nửa chu vi tam giác tiếp tục dựa vào công thức: ½P = (a+b+c) : 2

Ví dụ: Cho tam giác có tính nhiều năm 3 cạnh thứu tự là 4cm, 8cm và 9cm. Tính chu vi hình tam giác.

Dựa nhập công thức tất cả chúng ta sẽ sở hữu điều giải là Phường = 4 + 8 + 9 = 21cm

2. Công thức tính chu vi tam giác cân

Tam giác cân nặng là tam giác sở hữu 2 cạnh và 2 góc đều nhau. Đỉnh của tam giác cân nặng là skin của 2 cạnh mặt mũi.

Để tính chu vi tam giác cân nặng, các bạn cần phải biết đỉnh của tam giác cân nặng và phỏng nhiều năm 2 cạnh là được. Công thức tính chu vi hình tam giác cân nặng là:

P = 2a + c

Trong đó:

• a: Hai cạnh mặt mũi của tam giác cân nặng.
• c: Là lòng của tam giác.

Lưu ý, công thức tính chu vi tam giác cân nặng sẽ tiến hành vận dụng nhằm tính chu vi của tam giác vuông cân nặng.

Ví dụ: Cho hình tam giác cân nặng bên trên A với chiều nhiều năm AB = 7cm, BC = 5cm. Tính chu vi hình tam giác cân nặng.

Dựa nhập công thức tính chu vi tam giác cân nặng, tớ sở hữu phương pháp tính Phường = 7 + 7 + 5 = 19cm.

3. Cách tính chu vi tam giác đều

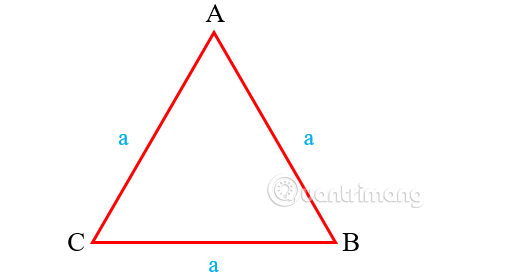
Tam giác đều là tình huống đặc biệt quan trọng của tam giác cân nặng Lúc 3 cạnh đều nhau. Công thức tính tam giác đều là:

P = 3 x a

Trong đó

• P: Là chu vi tam giác đều.
• a: Là chiều nhiều năm cạnh của tam giác.

Ví dụ: Tính chu vi tam giác đều phải sở hữu cạnh AB = 5cm.

Dựa theo đuổi công thức tất cả chúng ta sở hữu phương pháp tính Phường = 5 x 3 = 15cm.

4. Chu vi tam giác vuông

Tam giác vuông là tam giác có một góc vuông 90°. Công thức tính chu vi tam giác vuông là:

P = a + b + c

Trong đó

• a và b: Hai cạnh của tam giác vuông.
• c: Cạnh huyền của tam giác vuông.

Ví dụ: Tính chu vi tam giác vuông với phỏng nhiều năm CA = 6cm, CB = 7cm và AB = 10cm.

Xem thêm: tat ca hoat hinh

Dựa nhập công thức tính tất cả chúng ta sở hữu phương pháp tính Phường = 6 + 7 + 10 = 23cm.

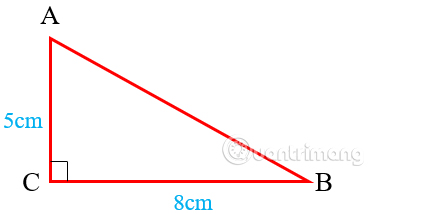
Ngoài đi ra tất cả chúng ta cũng hoàn toàn có thể tính chu vi của tam giác vuông lúc biết phỏng nhiều năm 2 cạnh. Cho tam giác vuông với chiều nhiều năm CA = 5cm, CB = 8cm, tính chu vi.

Như hình tiếp sau đây tự tam giác vuông ở C nên cạnh huyền là AB. Để tính cạnh huyền tam giác vuông cân nặng, tớ tiếp tục dựa vào quyết định lý Pitago nhập tam giác vuông.

AB² = CA² + CB²

AB² = 25 + 64

AB = 9,4cm

Vậy chu vi tam giác vuông CAB là:

P = 5 + 8 + 9,4 = 22,4cm

5. Chu vi tam giác nhập ko gian

Giả sử các bạn sở hữu Việc cần thiết tính chu vi tam giác nhập không khí như sau:

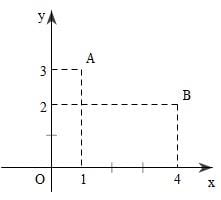
Bài toán: Trong không khí mang lại mặt mũi phẳng lì Oxy, sở hữu nhì điểm A(1;3), B(4;2).

1. Tìm tọa phỏng điểm D phía trên trục Ox sao mang lại DA=DB;
2. Tính chu vi tam giác OAB?

Tính chu vi tam giác nhập ko gian

Sau đấy là điều giải của Việc trên:

a. phía trên trục tọa phỏng nên tọa phỏng của là

Ta có:

b.

Xem thêm: kế hoạch cá nhân học tập và làm theo tư tưởng đạo đức phong cách

Chu vi tam giác .

• Trọng tâm là gì? Công thức tính trọng tâm của tam giác